공간(space)이라고 부릅니다.
확률공간(probability space)은 “표본공간”이라는 근원사건(elementary)의 집합(set)에 수학적 구조인 “사건들의 대수($\sigma$-algebra)”와 이 대수에 정의된 “확률측도(probability measuer)”를 추가합니다.
사건(event)은 근원사건을 원소로 하는 표본공간의 부분집합입니다.
“$\sigma$-대수”는 사건들의 유한 합집합에 대해 닫혀 있습니다.
확률공간에서 시그마-대수(代數)는 사건공간이라고도 부르며 사건들에 대해 합, 교, 여집합 등 집합 연산을 수행해도 그 결과가 항상 포함되는 체계입니다.
| 기호 | 명칭 | 의미 및 설명 | 예시(주사위 던지기) |
|---|---|---|---|
| Ω | 표본공간 (Sample Space) | 확률실험에서 가능한 모든 결과의 집합으로 “공간” 자체를 의미 | {1, 2, 3, 4, 5, 6} |
| $\mathcal F$ | 사건공간 (Sigma Algebra) | 표본공간 위에서 확률을 정의할 수 있는 사건들의 집합, 공간의 “구조”를 의미 | {{}, {짝수}, {홀수}, {1,2,3,4,5,6}} |
| $\mathrm P$ | 확률측도 (Probability Measure) | 사건에 대한 확률값을 부여하는 함수, 공간에서 사건의 크기를 재는 “측정 방법”을 의미 | P(짝수)=1/2, P({1})=1/6 |
| 확률실험 예시 | 표본공간(가능한 모든 결과의 집합, 근원사건의 집합) | 확률측도 모델링 예시 |
|---|---|---|
| 동전 던지기 | {앞, 뒤} | 베르누이분포 |
| 주사위 던지기 | {1, 2, 3, 4, 5, 6} | 이산균등분포 |
| 동전 두 번 던지기 | {(앞,앞), (앞,뒤), (뒤,앞), (뒤,뒤)} | 이항분포 |
| 시험 점수 측정 | 실수 구간 [0,100] | 스케일 변환 베타분포 |
| 센서의 측정오차 | 실수 전체의 집합 ℝ | 정규분포 모델 |
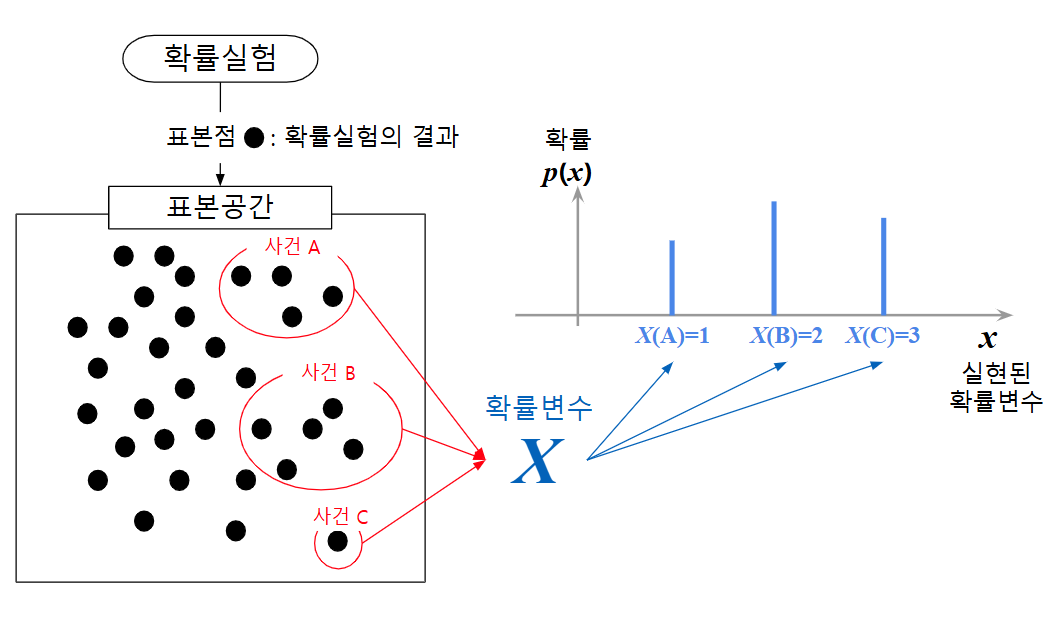
확률변수(random variable)는 확률공간의 표본공간에서 실수공간으로 가는 함수입니다.
$$X: (\Omega, {\mathcal F}, {\mathrm P}) \rightarrow({\mathbb R}, {\mathcal B})$$
여기서, $\Omega$는 표본공간(sample space)
${\mathcal F}$는 시그마 대수($\sigma$- algebra), 사건 공간
${\mathrm P}$는 확률측도(probability measure)
${\mathbb R}$은 실수 집합(real numbers)
${\mathcal B}$는 실수 위의 보렐 시그마 대수(Borel sigma algebra)
확률변수는 확률적 현상을 실수(real number)로 표현해 계산 가능하게 만듭니다. 이를 통해 기대값, 분산, 확률분포 같은 개념을 사용할 수 있게 됩니다.
표본공간이 벡터공간(예: ${\mathrm R}^n$)일 경우, 확률변수는 여전히 실수 공간으로 가는 스칼라 확률변수로 정의될 수도 있고, 또는 다른 벡터 공간으로 가는 벡터 확률변수로 정의될 수도 있습니다.