네, 그렇습니다.
다변량 표준정규분포 표본공간에서 표본평균점은 (1, 1, …, 1) 방향의 1차원 부분공간, $\operatorname{span}(\mathbf{1})$ 위에 존재합니다.
표본평균점에서 표본점까지의 거리(norm), $\| \mathbf{y}-\bar{y}\mathbf{1} \|$는 자유도가 $n-1$인 카이분포를 따릅니다.
$$\| \mathbf{y} – \bar{y}\mathbf{1} \| \sim \chi_{n-1}$$
표본의 원소가 표준정규분포를 나타내면, 표본공간 $\mathbb{R}^n$에 확률을 부여하여 다변량 표준정규분포로 표현할 수 있습니다.
표본의 원소가 서로 독립인 표본의 크기 n을 차원으로 하는 표본공간에서 표본평균은 벡터로 표현할 수 있습니다. 원점에서 표본평균점까지를 벡터로 표현할 수 있으며 모든 성분이 동일합니다.
\[
\mathbf{Y} = (Y_1, Y_2, \ldots, Y_n)^{\top}, \qquad Y_i \sim N(0,1)
\]
표본평균은 스칼라이며 다음과 같이 정의됩니다.
\[
\bar{Y} = \frac{1}{n}\sum_{i=1}^n Y_i
\]
표본평균의 분포는
\[
\bar{Y} \sim N\!\left(0, \frac{1}{n}\right)
\]
이를 정규화(normalizing)하면
\[
\sqrt{n}\,\bar{Y} \sim N(0,1)
\]
따라서 표본평균의 절대값은 다음과 같이 표현됩니다.
\[
\left| \sqrt{n}\,\bar{Y} \right| = |Z|, \qquad Z \sim N(0,1)
\]
정규분포 표본의 절대값은 자유도 1인 카이분포와 같습니다.
\[
|Z| \sim \chi_1
\]
따라서 원점에서 표본평균까지의 “거리”는 다음과 그림과 같은 관계를 가집니다.
\[
\sqrt{n}\,|\bar{Y}| \sim \chi_1
\]
또는 동등하게
\[
|\bar{Y}| \sim \frac{1}{\sqrt{n}}\,\chi_1
\]
다변량 표준정규분포에서 추출된 표본을 다음과 같이 표현할 수 있습니다.
$$
\mathbf{Y} = (Y_1, Y_2, \ldots, Y_n)^{\top}, \qquad Y_i \sim N(0,1)
$$
표본평균은 스칼라이며 다음과 같습니다.
\[
\bar{Y} = \frac{1}{n}\sum_{i=1}^{n} Y_i
\]
표본평균점에서 표본점까지의 편차벡터(deviation vector)는
\[
\mathbf{Y} – \bar{Y}\mathbf{1}
\]
이 편차벡터의 크기(norm)는
\[
\left\| \mathbf{Y} – \bar{Y}\mathbf{1} \right\|
\]
표본편차제곱합(sum of squared deviations)은 다음과 같습니다.
$$\sum_{i=1}^{n}(Y_i – \bar{Y})^{2}$$
따라서 편차벡터의 길이는
\[
\left\| \mathbf{Y} – \bar{Y}\mathbf{1} \right\|
=
\sqrt{\sum_{i=1}^{n}\limits(Y_i-\bar{Y})^2}
\]
이므로,
\[
\left\| \mathbf{Y} – \bar{Y}\mathbf{1} \right\|
\;\sim\;
\chi_{\,n-1}
\]
즉, $n$차원 표본공간에서 표본평균점을 중심으로 본 표본들의 편차(거리)가 이루는 거리는 자유도 \(n-1\)의 카이분포를 따릅니다.
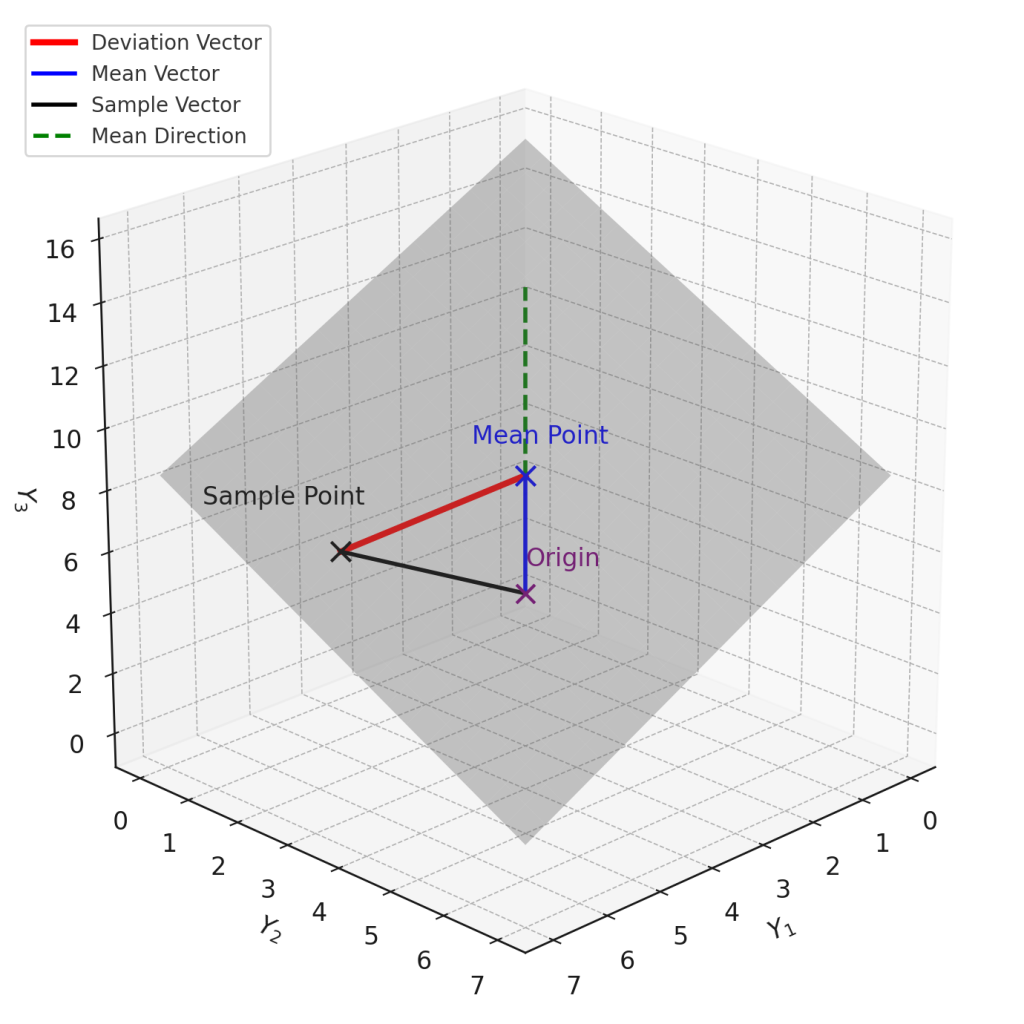
Figure 1. 평균선과 표본평균 평면과 편차벡터 시각화
1. 표본벡터의 분해
표본벡터는 다음식과 같이 평균성분과 편차성분으로 분해됩니다.
$$ \mathbf{Y} = \bar{Y}\mathbf{1} + (\mathbf{Y} – \bar{Y}\mathbf{1}) $$
여기서 $ \bar{Y}\mathbf{1} $ 은 표본평균을 모든 좌표에 반복한 벡터이며, $ \mathbf{Y} – \bar{Y}\mathbf{1} $ 은 평균에서 벗어난 편차 벡터입니다.
2. 분해의 의미
이 두 벡터는 $ (\bar{Y}\mathbf{1})^{\top}(\mathbf{Y} – \bar{Y}\mathbf{1}) = 0 $을 만족하여 서로 직교합니다.
이 분해는 ANOVA와 총제곱합(SS decomposition)의 핵심 개념이며, 데이터를 “평균 $ \bar{Y}\mathbf{1} $ + 편차 $ \mathbf{Y} – \bar{Y}\mathbf{1} $” 로 이해하는 통계학적 기반입니다. 또한 이 분해는 좌표축이 고정된 표본공간(sample space)에서 이루어집니다.
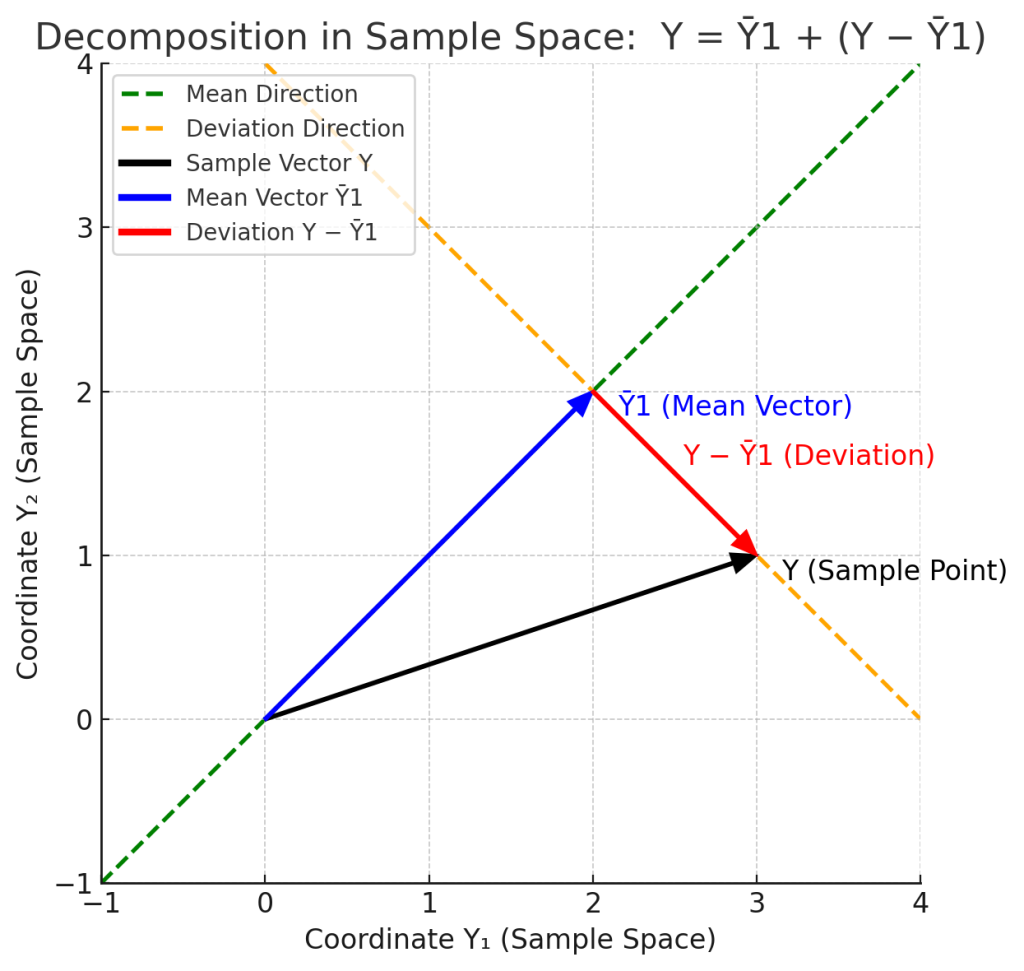
Figure 2. 표본공간에서 본 표본벡터의 평균·편차 분해
1. 표본편차제곱합의 직교분해를 수식으로 표현
표본벡터는 다음과 같이 정의됩니다.
$$\mathbf{Y} = (Y_1, Y_2, \ldots, Y_n)^{\top}$$
표본평균 방향의 1차원 부분공간으로의 투영은 다음식으로 표현할 수 있습니다.
$$\mathbf{P} = \frac{1}{n}\mathbf{1}\mathbf{1}^{\top}$$
표본평균 방향에 직교하는 ($n-1$)차원 부분공간으로의 투영은 다음과 같습니다.
$$\mathbf{M} = \mathbf{I} – \frac{1}{n}\mathbf{1}\mathbf{1}^{\top}$$
2. 직교분해 수식
표본벡터 $\mathbf{Y}$는 다음과 같이 직교분해됩니다.
$$\mathbf{Y} = \mathbf{P}\mathbf{Y} + \mathbf{M}\mathbf{Y}$$
직교성은 다음식을 만족합니다.
$$(\mathbf{P}\mathbf{Y})^{\top}(\mathbf{M}\mathbf{Y}) = \boldsymbol{0}$$
3. 표본편차제곱합이 제곱노름으로 표현되는 형태
표본편차벡터는 다음과 같습니다.
$$\mathbf{Y} – \bar{Y}\mathbf{1} = \mathbf{M}\mathbf{Y}$$
따라서 표본편차제곱합은 다음과 같이 표현됩니다.
$$\sum_{i=1}^{n}(Y_i – \bar{Y})^{2} = \|\mathbf{M}\mathbf{Y}\|^{2}$$
4. 표본편차제곱합의 의미
표본편차제곱합은 다음과 같이 정리됩니다.
$$\sum_{i=1}^{n}(Y_i – \bar{Y})^{2} = \|\mathbf{M}\mathbf{Y}\|^{2}, \quad
\text{여기서,} \,\, \mathbf{M} = \mathbf{I} – \frac{1}{n}\mathbf{1}\mathbf{1}^{\top}$$
$\mathbf{M}\mathbf{Y}$는 표본평균 방향에 직교하는 ($n-1$)차원 부분공간으로의 직교투영입니다. 이 벡터의 제곱노름은 표본편차제곱합과 동일합니다. 이는 ANOVA에서 표본편차제곱합의 자유도가 $n-1$이 되는 기하학적 이유를 제공합니다.
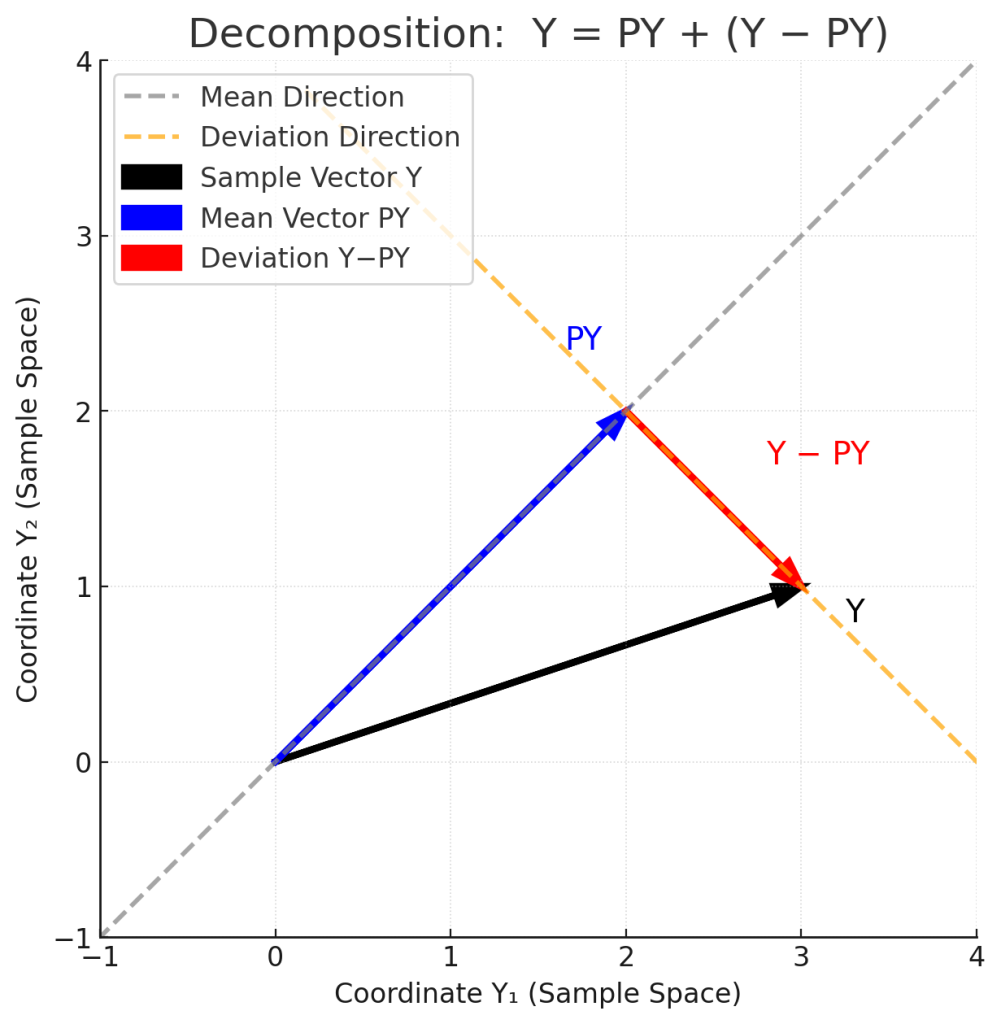
Figure 3. 표본벡터의 투영성분과 잔차벡터로의 분해